MatLab - Esercitazione #4 - Modello SS con matrici, Simulink, stimolo agli ingressi

Solite condizioni iniziali per pulire il Workspace, chiudere i file aperti e pulire l'editor.
clear all
close all
clc

%% Punto 1
Vengono inseriti i dati così come riportati dal testo
Ma = 290;
Mr = 60;
K = 20000;
Kp = 190000;
b1 = 1000;
b2 = 10000;

Matrice A ricopiata dal testo, espressa in forma simbolica
A = [   -b1/Ma  -K  b1/Mr   0;
        1/Ma    0   -1/Mr   0;
        b1/Ma   K   -(b1+b2)/Mr     -Kp
        0       0   1/Mr    0];

Matrice B ricopiata dal testo
B = [   -Ma 1   0;
        0   0   0;
        -Mr -1   b2
        0   -1  0];    

Matrice C ricavata: se y = (1/Ma)*Pa, allora la matrice C deve essere [1/Ma 0 0 0], essendo x sempre uguale a prima.
C = [ 1/Ma  0   0   0];

Matrice D è nulla, quindi 0 (no diretto legame fra entrate e uscite). Per D si può anche non stare attenti alle dimensioni, per il resto si.
Lanciata la simulazione nello spazio degli stati (comando ss).
sys = ss(A, B, C, 0)

%% Punto 2
Durata della simulazione (10 secondi)
Tfin = 10;
Condizione iniziale della simulazione (vettore colonna, quindi riga trasposta); queste vanno inserite nell'integratore.
X0 = [0 0.05 0 0]';

Sono dei vettori, quindi lettere maiuscole per convenzione.
Visualizzazione grafica del movimento libero: initial(sys,x0) (risposta libera del sistema); è da plottare XMa, ovvero y (da come si legge sul testo).
[Y, T, X] = initial(sys, X0, Tfin);

Creazione di una nuova figura, definizione del nome, della griglia e delle etichette degli assi.
h = figure;
set(H,'PropertyName',PropertyValue)
set(h, 'name', 'Evoluzione libera dell''uscita')
plot(T, Y)
Griglia
grid on
Etichette
xlabel('t')
ylabel('y')

%% Punto 3
Bisogna ottenere lo stesso risultato di prima utilizzando però ora il blocchetto LTI del Control System toolbox, quindi lavorando con Simulink. Le uscite sono Y1 e T1 per il tempo. Nel blocchetto viene dato come variabile di sistema "sys" (definita prima) e come condizione iniziale "X0". In entrata abbiamo segnale nullo (Ground).
In sostanza, una volta definita la variabile "sys" posso sia utilizzare la funzione initial oppure utilizzare gli strumenti grafici di Simulink per ottenere lo stesso risultato.
Simulazione dello schema di Simulink chiamato "untitled".
sim('untitled', Tfin)
Viene mantenuta la figura precedente.
hold on
Viene plottato il grafico sopra a quello di prima, ora però in rosso.
plot(T1, Y1, 'red')

%% Punto 4
Utilizzando sempre Simulink bisogna creare uno schema che permetta di accedere anche allo stato del sistema e non solo all'uscita (quindi non si può più utilizzare il blocchetto compatto).
Simulazione dello schema di Simulink chiamato "ss_model".
sim('ss_model', Tfin)
plot(T2, Y2, 'g-.')
h = figure;
set(h, 'name', 'Evoluzione libera dello stato');
subplot(RIGHE, COLONNE, POSIZIONE UTILIZZATA)
subplot(2, 2, 1);
plot(T2, X2(:, 1)) -> Tutta la prima riga di X2
grid on
ylabel('x1')

subplot(2, 2, 2);
plot(T2, X2(:, 2)) -> Tutta la seconda riga di X2
grid on
ylabel('x2')

subplot(2, 2, 3);
plot(T2, X2(:, 3)) -> Tutta la terza riga di X2
grid on
ylabel('x3')

subplot(2, 2, 4);
plot(T2, X2(:, 4)) -> Tutta la quarta riga di X2
grid on
ylabel('x4')

%% Punto 5
Si applicano ora condizioni iniziali di riposo.
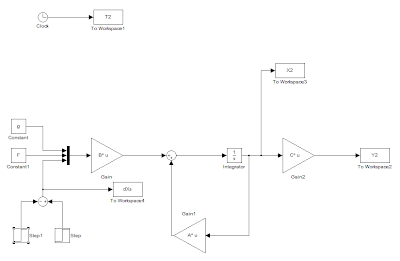
Si definiscono degli specifici ingressi: si utilizza lo stesso schema di prima, però si utilizza un multiplexer per avere gli ingressi con segnali differenti.
X0 = [0 0 0 0]';
g = 9.81;
F = 0;
L'ultimo ingresso ha una forma particolare: Xs(t) = h(t − 5) − h(t − 5.2), essendo h(t) la funzione gradino unitario; per fare questo si prendono due blocchetti step e un sommatore (+, -): il primo step in +, il secondo in -. Il primo ha come parametri di step time e final value 5 e 1, il secondo 5.2 e 1.
ts1 = 5;
as1 = 1;
ts2 = 5.2;
as2 = 1;

sim('ss_input_model', Tfin)
h = figure;
set(h, 'name', 'Uscita forzata del sistema');
plot(T2, dXs, 'red--');
grid on
hold on
plot(T2, Y2)